霍尔德镜像变换

Householder Transformation

Apr 11, 24

Householder Transformation

在线性代数中, Householder变换 (也称为Householder反射或镜面反射变换) 是一种描述关于包含原点 的平面或超平面反射的线性变换。

In linear algebra, a Householder transformation (also known as a Householder reflection or elementary reflector) is a linear transformation that describes a reflection about a plane or hyperplane containing the origin.

H=I−2wwTH = I - 2 w w^{T}

其中, ww 是一个单位向量, II 是单位矩阵。

Where ww is a unit vector and II is the identity matrix.

为啥能镜像

How does it work?

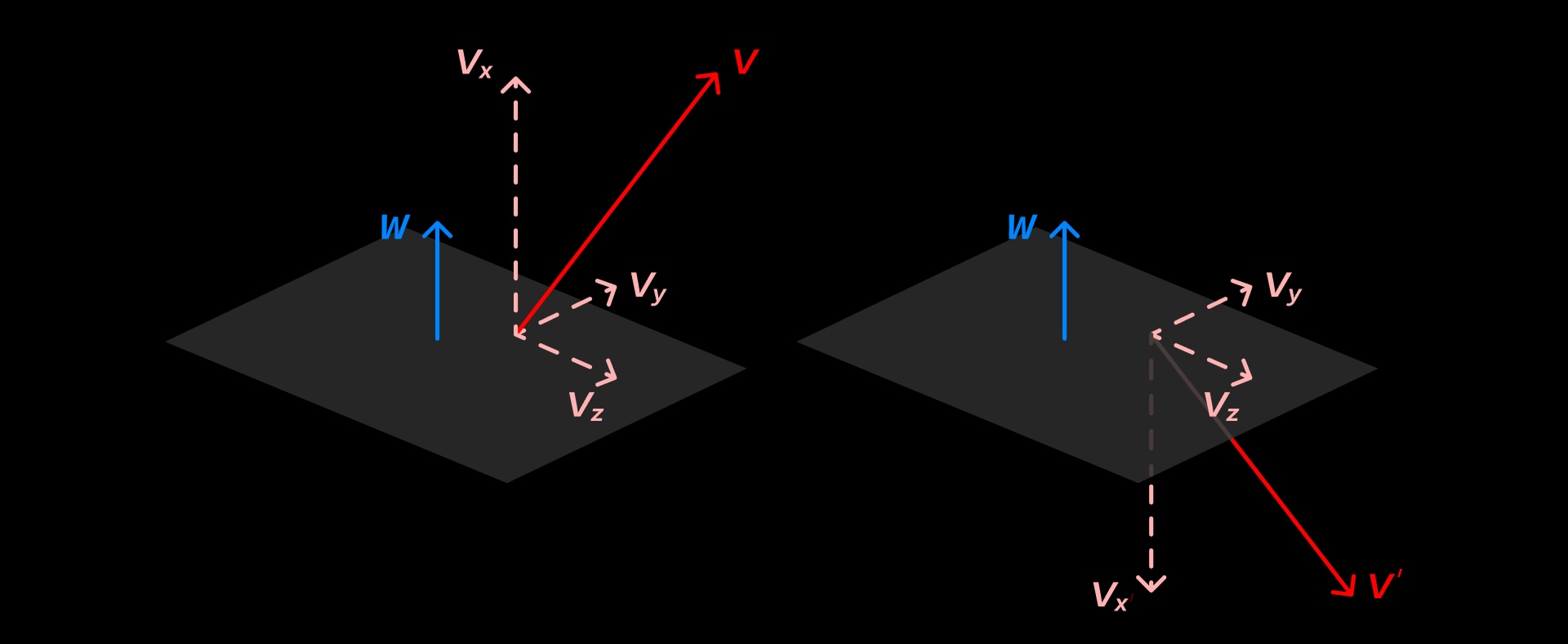
我们以最熟悉的三维空间为例, 如上图, 将 ww 想象为一个平面的法向量, 假设给定一个向量 vv, 将 vv 分解到一组正交基 {vx,vy,vz}\{v_x, v_y, v_z\} 上, 同时保证 vx=wv_x = w。这样的分解使得:

Let's take the 3-dimensional space as an example. As shown in the figure above, we think of ww as a normal vector of a plane. Suppose we have a given vector vv, we decompose vv onto a set of orthogonal basis {vx,vy,vz}\{v_x, v_y, v_z\}, ensuring that vx=wv_x = w. This decomposition meets:

w⋅vx=0w⋅vy=0\begin{aligned} w\cdot v_x &= 0\\ w\cdot v_y &= 0\end{aligned}

那么, vv 经过 Householder 变换后, 会变成:

Then, after the Householder transformation, vv will become:

Hv=(I−2wwT)(vx+vy+vz)=vx−2wwTvx+vy−2wwTvy+vz−2wwTvz=−vx+vy+vz=v′ \begin{aligned} Hv &= (I - 2 w w^T) (v_x + v_y + v_z)\\ &= v_x - 2 w w^T v_x + v_y - 2 w w^T v_y + v_z - 2 w w^T v_z\\ &= -v_x + v_y + v_z\\ &= v' \\ \end{aligned}

这样, vv 就沿着 ww 的法向量方向, 镜像到了 v′v' 上。

Thus, vv is mirrored onto v′v' along the normal vector of ww.